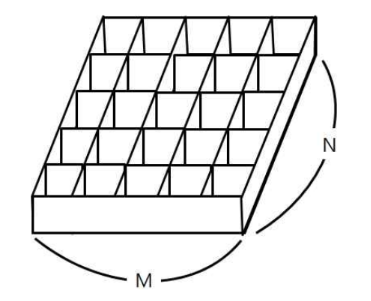
철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자모양 상자의 칸에 하나씩 넣은 다음, 상자들을 수직으로 쌓아 올려서 창고에 보관한다.
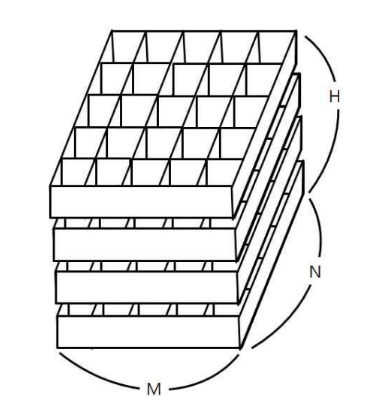
창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토에 인접한 곳은 위, 아래, 왼쪽, 오른쪽, 앞, 뒤 여섯 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지 그 최소 일수를 알고 싶어 한다.
토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.
입력
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N과 쌓아올려지는 상자의 수를 나타내는 H가 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M ≤ 100, 2 ≤ N ≤ 100, 1 ≤ H ≤ 100 이다. 둘째 줄부터는 가장 밑의 상자부터 가장 위의 상자까지에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 하나의 상자에 담긴 토마토의 정보가 주어진다. 각 줄에는 상자 가로줄에 들어있는 토마토들의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0 은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다. 이러한 N개의 줄이 H번 반복하여 주어진다.
토마토가 하나 이상 있는 경우만 입력으로 주어진다.
출력
여러분은 토마토가 모두 익을 때까지 최소 며칠이 걸리는지를 계산해서 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.
풀이
public class Main {
static int N, M, H;
static int[][][] field;
static Queue<int[]> queue = new LinkedList<>();
static int[] dx = {0,0,0,0,-1,1};
static int[] dy = {0,0,1,-1,0,0};
static int[] dz = {-1, 1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
M = Integer.parseInt(st.nextToken());
N = Integer.parseInt(st.nextToken());
H = Integer.parseInt(st.nextToken());
field = new int[N][M][H];
for (int h=0; h<H; h++){
for (int i=0; i<N; i++){
st = new StringTokenizer(br.readLine());
for (int j=0; j<M; j++){
field[i][j][h] = Integer.parseInt(st.nextToken());
if (field[i][j][h] == 1){
queue.add(new int[]{i,j,h});
}
}
}
}
int max = 0;
BFS();
}
static void BFS(){
int count = 0;
while (!queue.isEmpty()){
int[] point = queue.poll();
for (int i=0; i<6; i++){
int nx = point[0] + dx[i];
int ny = point[1] + dy[i];
int nz = point[2];
if (i < 2){
nz = point[2] + dz[i];
}
if (nx >= 0 && ny >= 0 && nz >= 0 && nx < N && ny < M && nz < H){
if (field[nx][ny][nz] == 0){
field[nx][ny][nz] = field[point[0]][point[1]][point[2]] + 1;
count = Math.max(count, field[nx][ny][nz]);
queue.offer(new int[]{nx,ny,nz});
}
}
}
}
if (check()){
if (count == 0){
System.out.println(count);
} else{
System.out.println(count -1);
}
} else {
System.out.println("-1");
}
}
static boolean check(){
for (int i=0; i<H; i++){
for (int j=0; j<N; j++){
for (int k=0; k<M; k++){
if (field[j][k][i] == 0){
return false;
}
}
}
}
return true;
}
}해설
https://choincnp.tistory.com/95
[백준/7576] - 토마토(JAVA)
철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자 모양 상자의 칸에 하나씩 넣어서 창고에 보관한다. 창고에 보관되는 토마토들 중에는
choincnp.tistory.com
기존의 토마토 문제에 상하 위치만 추가된 문제이다.
시작점이 여러개이므로 큐를 클래스 변수로 선언하고, 가로 세로 상단에 맞추어 field에 토마토를 담은 뒤
BFS를 돌려주면 되는 문제이다. 물론 BFS를 재귀 형태로 돌려주어도 되지만, 델타배열로 선언하였다.
BFS의 Well-Known 문제로, 특별히 어려운 점은 없는 문제이다.
'알고리즘 > 백준' 카테고리의 다른 글
| [백준/2143] - 두 배열의 합(JAVA) (0) | 2023.09.27 |
|---|---|
| [백준/2573] - 빙산(JAVA) (0) | 2023.09.20 |
| [백준/14502] - 연구소(JAVA) (0) | 2023.09.19 |
| [백준/7576] - 토마토(JAVA) (0) | 2023.09.19 |
| [백준/1697] - 숨바꼭질(JAVA) (0) | 2023.09.18 |